What is the Handshaking Lemma?
Imagine a small party where people are shaking hands. The Handshaking Lemma offers a simple rule: if you add up the number of hands each person shook, the total sum will always be an even number.
In graph theory, we replace people with "vertices" (dots) and handshakes with "edges" (lines connecting the dots). The number of edges connected to a vertex is called its "degree."
The Formal Statement of the Handshaking Lemma:
For any undirected graph G = (V, E), the sum of the degrees of all vertices is equal to twice the number of edges.
Mathematically, this is expressed as:
Σ deg(v) = 2|E|
Where:
- Σ is the symbol for summation.
- deg(v) is the degree of a vertex v.
- |E| is the total number of edges in the graph.
This foundational formula is a must-know if you want to complete your math assignment in graph theory.
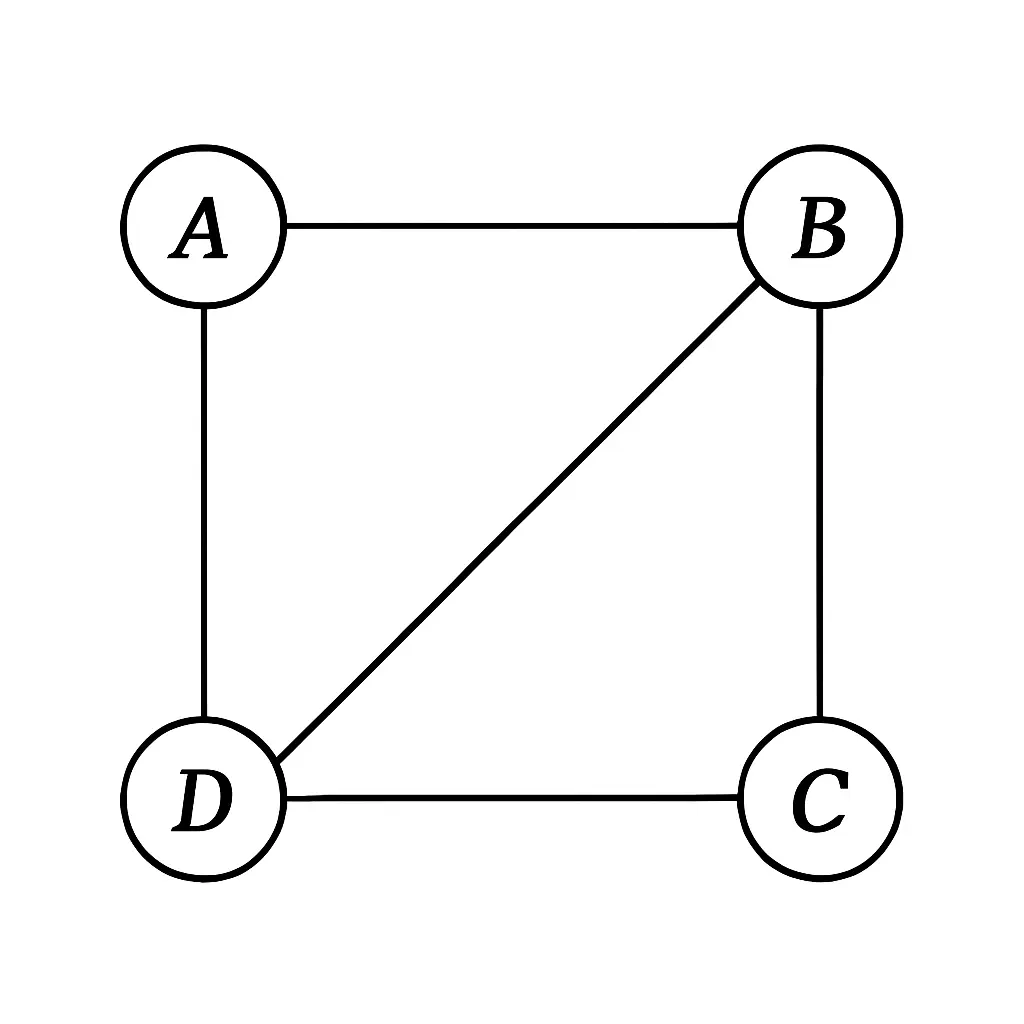
Alt Text: Graph with four nodes labeled A, B, C, and D, with edges connecting each pair of nodes in a complete graph.
- Vertex A is connected to B and D.
- Vertex B is connected to A and C.
- Vertex C is connected to B and D.
- Vertex D is connected to A and C.
There are a total of 4 edges: (A,B), (A,D), (B,C), and (C,D).]
Let's apply the lemma to the visual example above:
- Degree of A: 2
- Degree of B: 2
- Degree of C: 2
- Degree of D: 2
- Sum of Degrees: 2 + 2 + 2 + 2 = 8
- Number of Edges (|E|): 4
- The Lemma holds: 8 = 2 * 4
Proof of the Handshaking Lemma
The proof is beautifully intuitive. If you need help with your math assignment involving proofs, this breakdown will make it click.
- Consider a single edge. By definition, every edge connects two vertices.
- Count its contribution. When we sum the degrees of all vertices, this single edge gets counted twice: once for the degree of the first vertex it connects, and a second time for the degree of the second vertex.
- Total contribution per edge. Therefore, each edge in the graph contributes exactly 2 to the total sum of degrees.
- Sum over all edges. To find the total sum of degrees for the entire graph, we simply multiply the number of edges by 2.
Thus, Σ deg(v) = 2|E|.
A key takeaway from this is that in any graph, the number of vertices with an odd degree must be even. It's impossible to add up an odd number of odd numbers and get an even total!
Practical Applications of the Handshaking Lemma
This isn't just an abstract rule; it has real-world uses:
- Network Integrity: In computer networks, it helps verify that a network map is correct. If the sum of connections is odd, there's an error.
- Molecular Chemistry: Atoms can be modeled as vertices and bonds as edges. The lemma validates the structure of chemical compounds.
- Data Structures: The principle is fundamental in computer science for algorithms related to trees and graphs.
Why Choose My Perfect Writing for Your Mathematics Assignment Help?
Expert Tutors
Our team at My Perfect Writing includes professional mathematicians who excel in discrete mathematics. When you need someone to do your math assignment for you, you're getting support from a true subject matter expert.
Step-by-Step Solutions
We provide detailed solutions that explain the logic behind each step. This approach is perfect for students seeking high-quality mathematics assignment help that also serves as a learning tool.
Comprehensive Online Support
Stuck on a problem at midnight? We provide reliable online math assignment help 24/7. Students searching for assignment help in math can count on us for timely and accurate solutions, regardless of the deadline.
Plagiarism-Free and On Time
Every solution is created from scratch to ensure it's 100% original. We pride ourselves on delivering top-notch work right when you need it.
Table: Key Graph Theory Concepts at a Glance
|
Concept |
Simple Description |
Relevance to Handshaking Lemma |
|---|---|---|
|
Vertex (or Node) |
A point or a dot in the graph. |
The lemma sums the degrees of all vertices. |
|
Edge (or Arc) |
A line connecting two vertices. |
The sum of degrees is 2x the number of edges. |
|
Degree of a Vertex |
The number of edges connected to it. |
This is the core property summed in the lemma. |
|
Undirected Graph |
A graph where edges have no direction. |
The Handshaking Lemma applies to these graphs. |
Ready to Master Graph Theory?
Don't let complex graph theory problems hold you back. Whether it's the Handshaking Lemma or more advanced topics, My Perfect Writing is your trusted partner for clear, effective, and reliable math assignment help.
Get Expert Math Assignment Help Today!
Frequently Asked Questions
What is the Handshaking Lemma in simple terms?
In any network, if you add up the connections for every point, the total will be an even number—specifically, twice the total number of connections.
Can you help me with graph theory proofs for my assignment?
Absolutely! My Perfect Writing experts specialize in discrete mathematics and can provide clear, step-by-step proofs. Our online math assignment help service is perfect for tackling tough theoretical questions.
Is your service suitable for all discrete mathematics topics?
Yes. We offer comprehensive help across discrete mathematics, including graph theory, combinatorics, set theory, and logic.
How do I get My Perfect Writing to do my math assignment?
It's easy! Visit our website, submit your assignment requirements, and get a quote. Once you confirm, our experts will begin crafting a high-quality, original solution tailored for you.
Can My Perfect Writing help with graph theory topics like the Handshaking Lemma?
Yes! Our expert mathematicians can guide you through graph theory concepts such as the Handshaking Lemma, vertex degrees, adjacency matrices, and more. We provide step-by-step explanations and fully worked solutions to help you understand and complete your math assignment with confidence.
Meet Our Professional Essay Writers
Empowering Your Academic Writing Journey with Authority, Expertise, and Experience
Dr. Emma Wilson
PhD in Literature
Prof. James Chen
MSc in Computer Science
Dr. Sarah Ahmed
PhD in Law & Ethics
Ready to Work With Our Expert Writers?







